品質工学の計算式の基本になっているy=βMの計算式について解説します。
パラメータ設計では、このSN比と感度を計算して評価していますが、MTシステムのT法やRT法においても、同じくy=βMの計算式が基礎になっています。(後述)
信号M(k個)に対する出力yに誤差N(2水準)を与えたデータの例で示します。
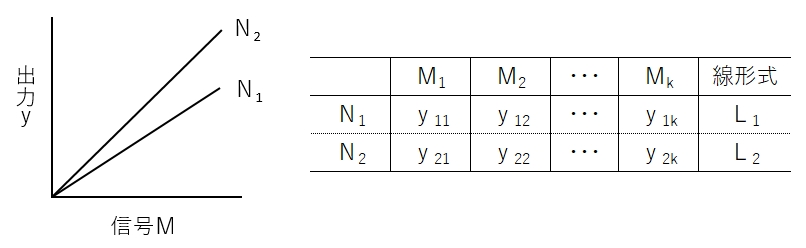

データの全変動(ST)を一次効果(Sβ)と調合誤差変動(SN×β),偶然誤差変動(Se)に分解しています。(2乗和の分解については こちら を参照してください)
SN比はばらつきの逆数です。(分子が出力βの2乗,分母はばらつきσの2乗)
よって、SN比は基本大きい方が良いと見ます。
感度はβの2乗で出力の大きさです。
基準点比例式
y=βMに乗らないデータもあります。信号に対する出力が比例関係でありながらゼロ点を通らない場合です。
このようなデータに対して、一次式のSN比というものも定義されています。「品質工学講座3・品質評価のためのSN比」に掲載されていますが、私はあまり使われたのをみたことがありません。どちらかというと基準点比例に置き換えて計算することが多いように思います。具体的にどのようにするかというと、
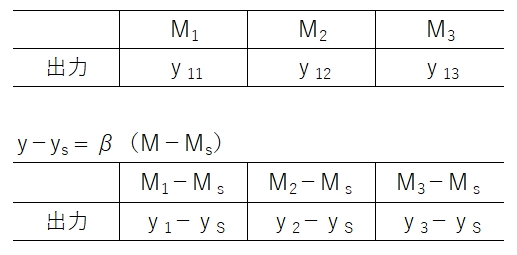
表のようなデータに対して、基準位置(Ms)を差し引いてデータを変換しておくのです。以降の計算は上述と同じでいけます。標準的なy=βMの計算で対応できるように変換することが、考え方に統一感があってわかりやすいようになっています。標準SN比も同じですね。
基準点比例の場合は、どこを基準にとるかが大切です。通常はM2の中間点をとることが多いでしょう(Ms=M2,ys=y2で計算します)。M1のほうがばらつきが安定していればMs=M1にする、などケースバイケースでMsを決めます。
T法(1)(2)は基準点比例式を適用しています。単位空間の平均値を計算し、信号データから平均値を引くという手順をとることで、単位空間の平均値を基準点とした計算をしています。T法(3)=RT法は単位空間の平均値を信号として計算しています。T法(Taguchi法)はy=βMの計算を判別分析に応用した手法ということができます。
そう考えると、重み付け計算の仕方がT法(1)と類似するH法はy=βMを扱っていないのでT法とは異なるということになりますね。