パラメータ設計は、ロバストデザインとか2段階設計などと呼ばれていますが、何を計測評価するかを決めて設計条件を直交表に割り付けて実験するものです。細かい計算式は省き、実験の流れについてのみ説明します。
ネックシステムの着眼
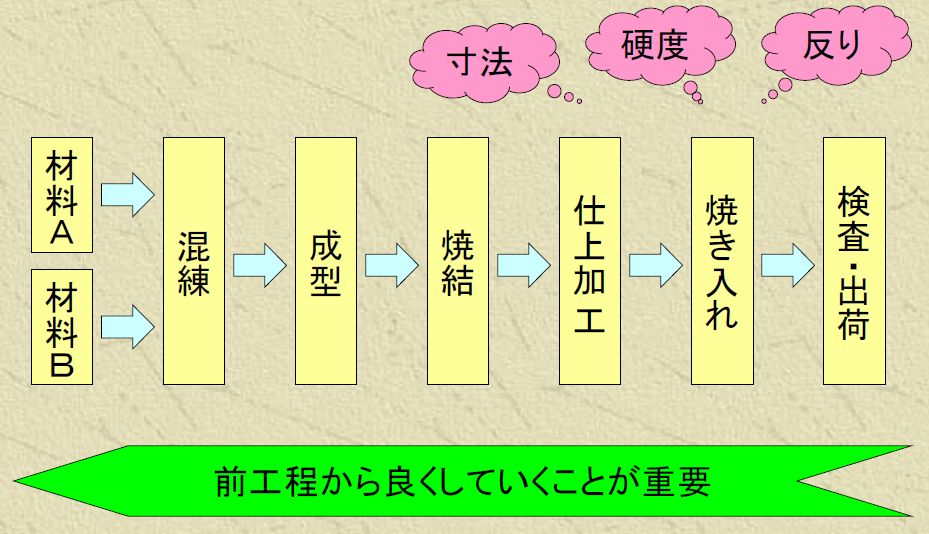
実験の計画を決めるとき、まずどこの工程をどの範囲で着手するかを決めます。例えば下図の場合、粉末冶金の工程の例ですが、寸法精度や反りといった品質特性を改善したいとしたとき、目先の工程は直接的に変形の起こる「焼き入れ」工程に手をつけたいだろうと思います。確かに熱収縮のタイミングで変形は起こるのですが、温度分布の安定化だけでは限界があります。それよりも前工程に遡って材料構成や混練条件の影響のほうが大きいことがよくあります。材料に混合ムラがあるから後工程の加熱で変形するのです。均一分散していれば反りは減るとイメージできますよね。このように工程全体を見渡して検討することが重要です。最近は「全体最適」という考え方が主流となってきており、一工程の部分最適ではなく、工程全体で最適化すべきだという事例が増えています。下図の工程の場合は最初の材料配合の工程から焼き入れ工程まで、各工程からいくつかずつ制御因子をピックアップして直交表に割り付ける、といったやり方です。
目的機能の明確化
性能の善し悪しを判断するのに、品質特性を評価していてはダメだと言われます。先の例で言う寸法精度や反りという「改善したい品質」をそのまま測定してはダメなのです。パラメータ設計の場合は効果に加法性があることが必要なので、基本機能で評価しなければなりません。
しかし、いきなり基本機能を考えるのは難しいことです。そこで、まず目的機能を定義します。そのほうが次のSTEPに行きやすいし、最悪、基本機能を思いつかなかったりまたはその計測を実現できなかったときには目的機能を評価してもうまくいく場合があるからです。
目的機能はy=βMの信号と出力で考えます。例えば、
・切削加工であれば 信号M:ネライの加工寸法 出力y:加工された寸法
・スクリーン印刷であれば 信号M:版寸法 出力y:印刷された寸法
基本機能の決定
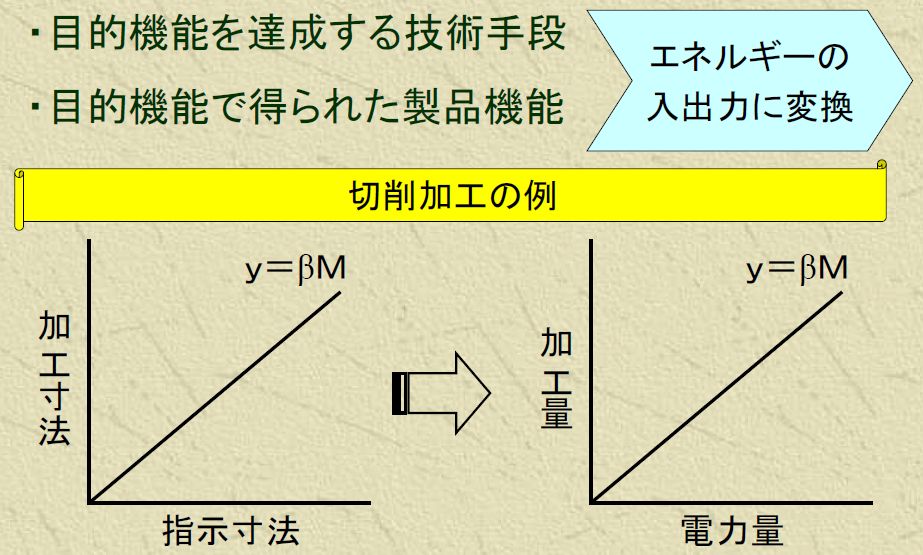
目的機能をさらに発展させ、よりシステムの原理に近い部分=基本機能を定義します。ヒントは、できるだけエネルギー変換になるような機能を考えることです。加工を例にあげると、例えば切削や旋削加工の場合、目的機能は[入力]指示寸法-[出力]加工された寸法ですが、これをエネルギーの入出力で考えると、入力(電力量)-出力(仕事量=加工重量)となります。これが加工の基本機能としてよく知られています。
誤差因子の決定
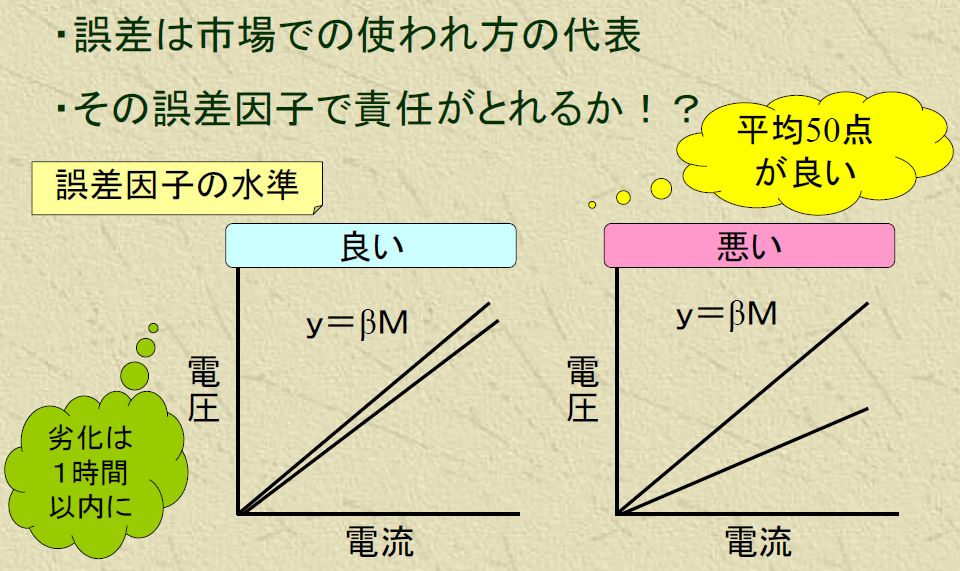
誤差因子は市場での使われ方です。劣化などが多く用いられます。劣化は、一般的な耐久試験のような条件では時間がかかり開発が間に合わないので、加速した条件を検討します。「1時間でできる劣化を考えろ」などとよく言われたものですが、18条件全部まとめて一晩くらいなら大丈夫です。それ以上かかるようなら、何か工夫できるところは残っていると思います。いかに効率的で充分な劣化を与えることができるか、各企業の技術ノウハウになる部分です。製造工程内の課題の場合は、目的機能のβが大きくなる条件と小さくなる条件の2条件で決めます。劣化であれ、工程内誤差であれ、適度に機能に影響するくらい(欠測がでない程度に大きく性能が落ちるくらい)が良いでしょう。その程度を予備実験などで確認してから誤差の与え方を決めるという手順が安全です。
テストピースの検討
実験は、製品形状でなくテストピースで行うのが理想です。
・先行性のある条件を評価できるようにする。
・多くの製品に適用できるようにする。(汎用性)
・計測しやすいようにする。(評価の効率化)
実際に流れている製品を流用して実験を行ったほうが手軽で早いという場合も多いと思いますが、先行性・汎用性を考慮したテストピースで実験することをオススメします。
制御因子の抽出
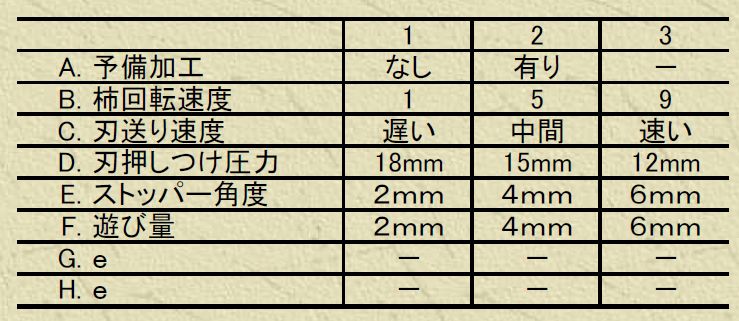
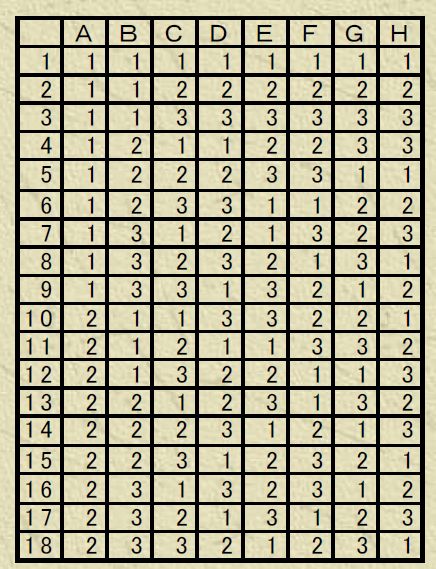
設計条件や製造条件で、改善するための因子と水準を決めます。主に直交表L18を使いますが、そこに割り付けることができるのは2水準1因子+3水準7因子で合計8因子です。下のような表で表現することが多いです。なお、8因子まで思いつかない場合、残りを誤差列(図のeの部分)にすることもできますが、改善のチャンスを失うことになるので、できるだけ全ての列を埋めるように制御因子を割り付けるほうが良いです。
水準決定と水準ずらし
制御因子の各水準の値は、可能な範囲で広い幅をとると良いです。なお、制御因子間の交互作用が強くありそうば場合、水準ずらしも考慮します。例えば温度と時間を制御因子に割り当てた場合、温度によって時間のきき方が変わってくるので、温度ごとに時間の水準値を変えたりします。
実験の実施
直交表の順序にもとづいて実験(サンプル製作~計測)を行います。制御因子(A~H)をどの水準にするか、直交表に従います。合計18種類の実験(サンプル製作など)を行いますので、少し大変ですが、後から得られる情報量を考えるとやる価値はおおいにあると思います。なお、実験の順序はランダマイズする必要はなく、やりやすい順番で行って大丈夫です。
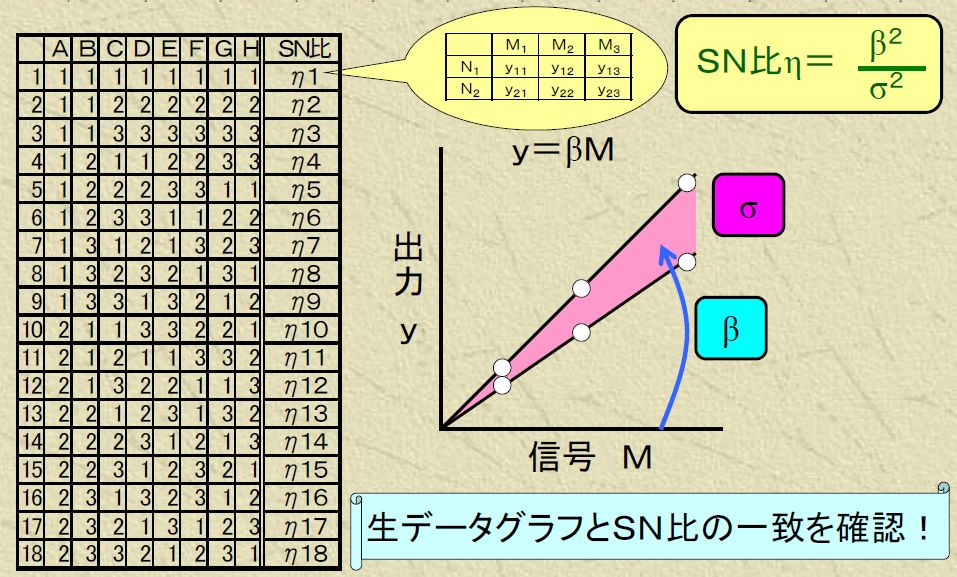
実験データの解析
各行毎にSN比と感度を計算します。測定データは18条件全て行毎にグラフ化しておくと良いでしょう。グラフのイメージと計算したSN比が合っているかを確認しておくことも大切です。
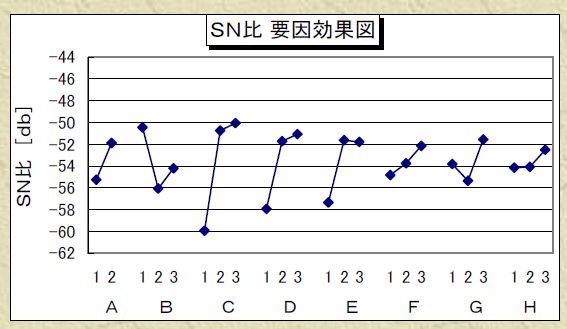
18行全てのSN比を計算したら、各因子の水準毎の平均値を求め、その値をグラフ化します。そのグラフは要因効果図と呼ばれています。このグラフでみる水準の傾向で、(水準値が連続量のときに)山形や谷形があると、その大きさ分だけ予想できていない誤差の影響がある可能性が高いです。
最適条件と利得の推定
確認実験による実験の検証を行うため、最適条件と比較条件を決めます。最適条件はSN比が最も高くなる条件です。比較条件は、現行条件でも良いです。(現行条件にすれば、現在よりどれくらい改善できるかがわかりやすいので)実験の検証という観点では、確認したい制御因子の水準を選ぶと良いでしょう。
確認実験
最適条件と比較条件で実際にサンプルを製作して、推定した値とどれくらい合致するか確認します。合致度が悪い場合、ここまで作成した要因効果図はほとんど信用できないと烙印をおされたことになるので、まずは要因効果図を廃棄してください!そして、再現しなかった理由を検討して、再計算程度ですめば良いのですが、最悪は実験のやり直しということもあり得ます。
目標値へのチューニング
最も重要なのはSN比によるばらつきの改善ですが、感度も改善のためには必要になることもあります。その場合、SN比に影響しない因子をつかって感度を調します。SN比にきく因子は固定条件で、SN比に影響しないけれど感度にきく因子は、量産適用してから製造工程で調整用に使ってもよい因子となります。
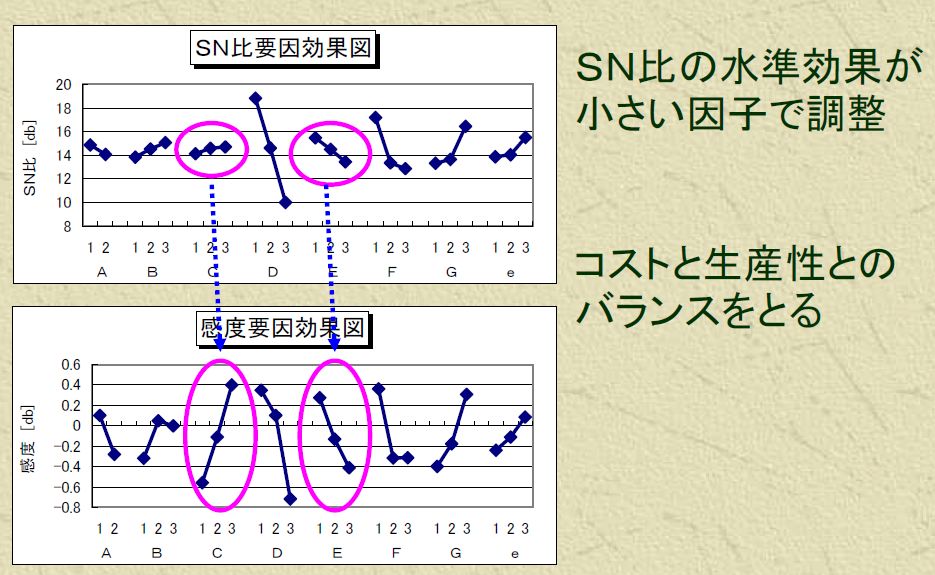
さらなる最適条件の追求
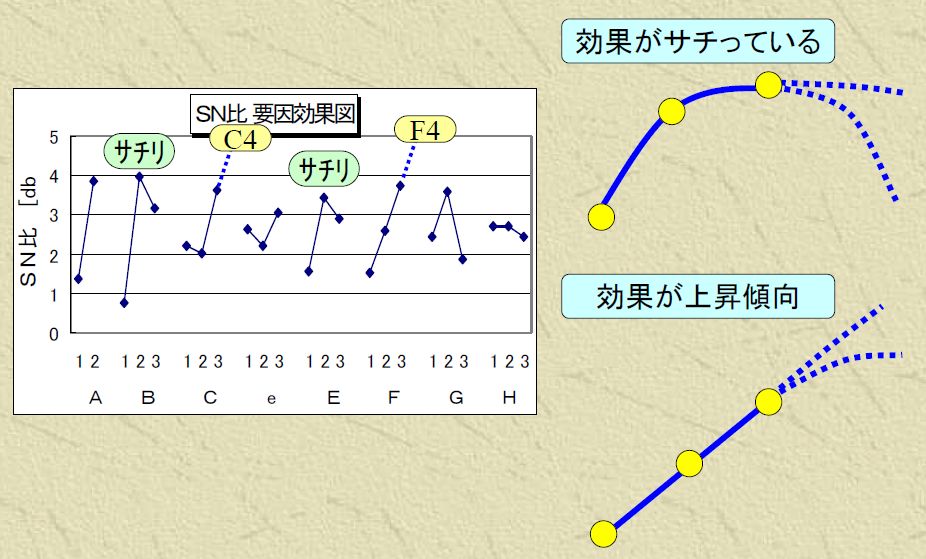
実験した範囲での最適条件よりもさらに良い条件が得られる可能性があります。水準傾向がサチり形でなく、均等上昇のような形の場合、さらに水準値をその方向に振ることができれば、最適条件よりもっと良くなる可能性があります。1因子多水準実験などで個別に確認してみると良いでしょう。
技術情報の標準化
実験で得られた情報を標準化します。前項にも記しましたが、製造工程で変えてはいけない条件と調整に使っても良い条件を明確にすることが大切です。
もっと詳しく知りたい方へ
実務に取り入れたい方は、こちら をご参照ください。
