ボリンジャーバンド(Bollinger Bands)頭文字をとってBBと表現することもあります。計算式は、標準偏差を計算して平均値に加算減算するわけですが、多くの書籍やネットの説明に私は疑問を感じていることろがあるので少し補足します。
標準偏差を計算して得られる値は、1σと表現されたりします。データが正規分布に従う場合、サンプルのデータが平均値の±1σに入る確率は68.3%と計算されます。これは品質管理の確率分布の計算からくるもので、同様に±2σは95.4%,±3σは99.7%と算出され、企業の品質管理では、(検査の合否判定規格に対する製品のばらつきが)3σは最低ラインで、4σや5σを目指すようになっています。図を見てわかるように、両側に外れる可能性があります。SQC(統計的品質管理)では片側にしかズレない場合には外れる確率を半分にして検定します。
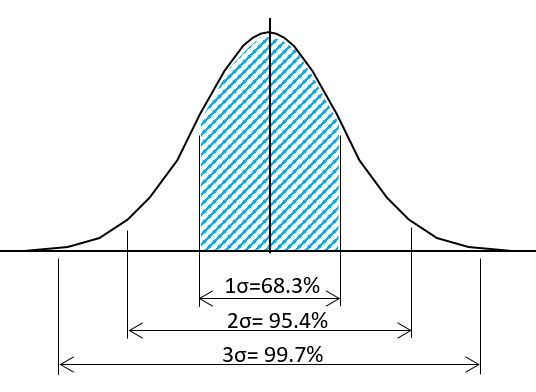
この確率は、正規分布に従うことが絶対条件です。企業で製造される製品のばらつきは正規分布に近似することが多いでしょう。
しかし、株価チャートのデータに標準偏差のこの確率を適用するのは間違いです。時系列的に変動するデータが正規分布になるとは思えません。少なくとも確率の値については間違いだと思っています。クレームをつけるつもりはありませんが、いつも違和感を感じる次第です。
では、ボリンジャーバンドの計算は間違いなのか?というと、、
私はBBの計算とグラフ化は役に立つと思っています。確率の値が誤りであるだけで、データを標準偏差で計算することは面白いと思うし、何より世の中で多くの人が使っている指標なら、それが正になるのです。
いろいろな使われ方が書籍やネットで紹介されています。どれも使ってこられた方の考え方で参考になると思います。私はそれほど使いこなせていないので、スクィーズとエクスパンジョンを見る程度のみですが、チャートには1~3σまで表示しています。