特徴
MT法では計算できない場合があります。
・多重共線性がある(相関係数が高すぎる項目がある)
・データ数に対して項目数が少ない
また、計算が煩雑で時間がかかるので、リアルタイムに結果を求められる場合に不向きです。
RT法はMT法のデメリットが改善された計算方法です。
メリット
・多重共線性やデータ数などによる制限がない
・計算が簡単なため処理速度が速い
デメリット
・MT法よりも精度が劣る可能性がある
MT法は相関関係を評価していますが、RT法は相関関係は 全く考えず項目ごとの誤差のみで評価しています。
計算式の考え方
単位空間(基準となるデータ群)の項目毎の平均値を信号としてSN比と感度を求め、SN比と感度の相関行列を作ります。比較したいデータは、同様にデータのSN比と感度を計算し、単位空間の行列から距離を計算します。
具体的な計算手順
・評価したいデータを準備する(項目を決める)
・基準となるデータと比較したいデータを分ける
※何を基準と考えるかが重要!基準となるデータを単位空間データと呼ぶ
・項目毎に平均値を求める
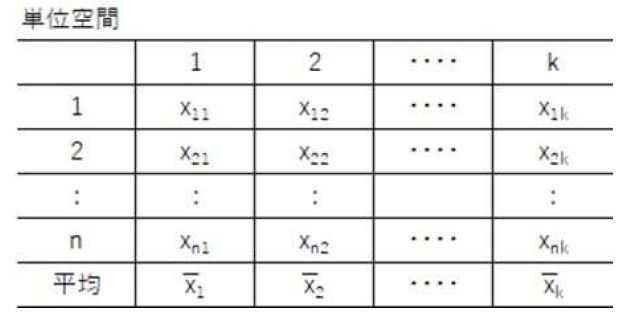
・項目ごとにSN比ηとβを求め、 Y1とY2を計算する
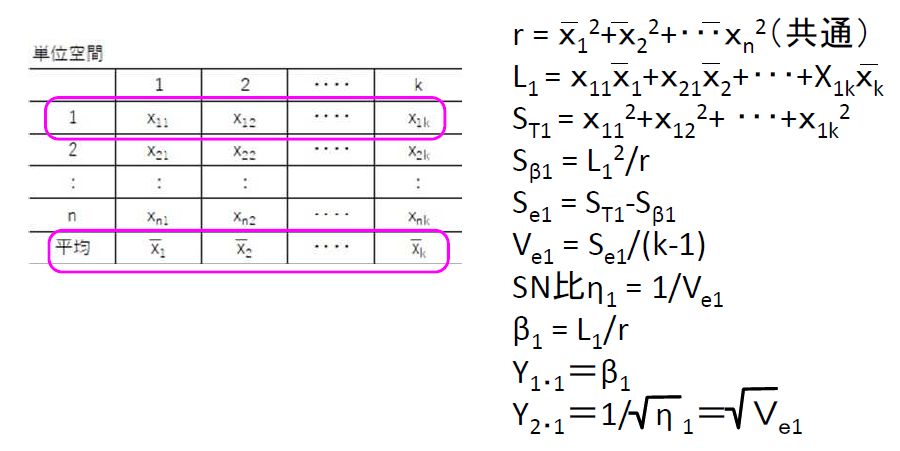
・Y1とY2から分散共分散行列Vを求める
・分散共分散行列の余因子行列Aを求める
・項目毎に距離Dを求める
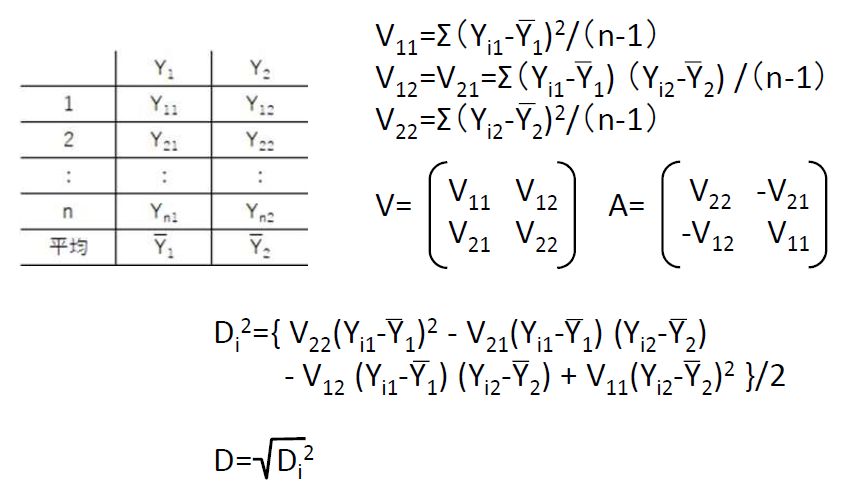
・同様に比較データ(又は信号データ)についても距離Dを求める
注)
有効除数rは単位空間の平均値から求めた値を使用する
余因子行列は単位空間で求めたものを使用する
・ヒストグラムなどで単位空間と比較データとの距離の差を
確認して、閾値を決める
※ヒストグラムにこだわりません。差が明確に表現されればOKです。
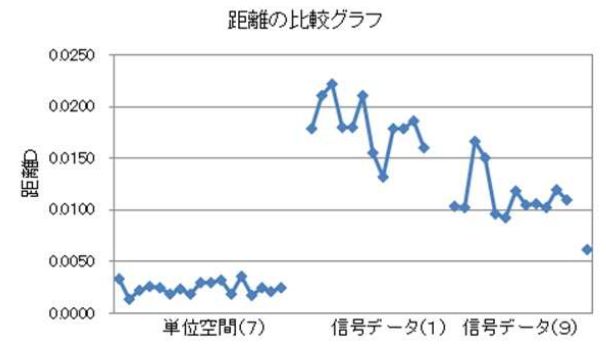
このグラフは、数字認識のお試しデータで計算してみたもので、7を単位空間にして 1 や 9 を正しく区分けできるかやってみたものです。