特徴
これは、一般的な品質工学の公式ではないので、計算式などは市販の本に掲載されていません。
仕事上のある課題をMTシステムを使って改善しようとして、うまくいかなかったため、結果を出すために独自に考案された計算方法です。H法の”H”は「過去データを利用するからHistoryのHだ」という人もいれば「発案者のイニシャルからとったものだ」という人もいます。T法(1)と計算の考え方が近いのですが、品質工学会の公認ではなく、今は一部の研究会でのみ研究されています。私は結果を出すことを最重要としているので、自分の仕事で成果を上げるために今も活用しています。
計算式の考え方
考え方は、熟練者の判断の仕方をイメージしていただくと良いと思います。
熟練者はいろいろな性状の製品について、経験と知識から(昔に作ったときの結果などを記憶していて)過去の実績を思い出しながらさじ加減を変えていきます。つまり、過去の性状と結果のデータベースから近いものをよりすぐり、それらの情報を統合する方法を考えました。「過去に似た製品があれば、求めたい値はそのときの製品による実績と近似する」が成立することが前提条件となります。
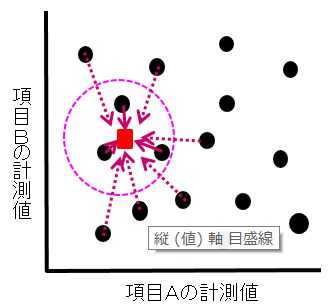
わかりやすいよう2項目だけの場合のイメージ図を下に示します。
推定したい条件の座標(図の■)を入れた時、その近さで重みづけします。たとえば近い3点で推定する場合、近さの比率を仮に50%,35%,15%としたとき、最も近い点の真値×50%+2番目に近い点の真値×35%+3番目に近い点の真値×15%で推定値を計算します。 なお、ここでいう真値(図の●がもつ値)は、絶対に正しい値ではありません。過去の実績であり、そこにはばらつきが含まれます。同じ条件でも前回と今回で全く同じ値にはならない可能性があります。よって、できるだけ多くの類似品で推定したほうが正しい値に近づくと考えます。
具体的な計算手順
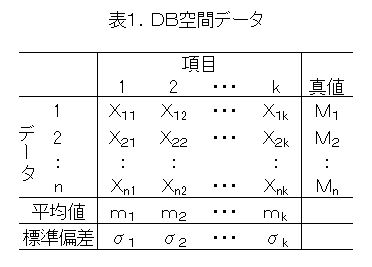
1)DB空間となるべきデータを集める(n個)
データ数は、できるだけ多くの条件が含まれていることが望ましいです。ただし、固定した条件でn数が多いと、それに近い条件はそのときの結果に引っ張られやすいので、条件毎のデータ数は均一になるほうが理想ではありますが、まずは基準となるデータを集めることを優先しましょう。異常値(原因不明の工程異常で変な値になったなど)を混ぜないことが大切です。
集めたデータを表1に示します。表1の「項目」とは、予測のための情報でk個,真値(M)は求めたい特性値でn個とします。
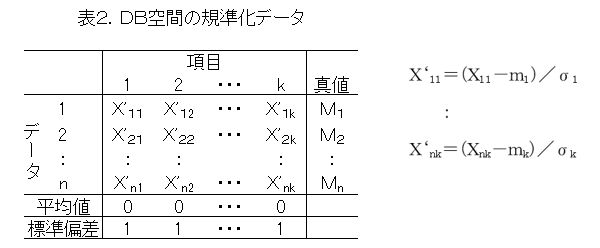
2)データを規準化する。
3)多次元の座標差を求める
推定値を求めたいものの項目値を規準化し、DB空間の規準化した値それぞれから差し引きます。

4)差分の分散を求める
5)SN比 η を求める
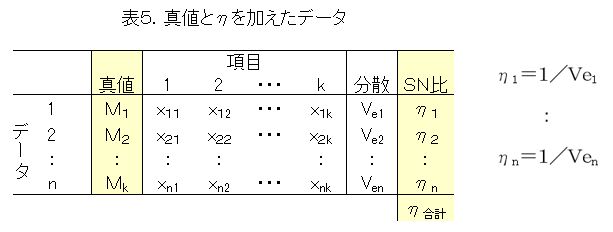
この時、推定したいデータと全く同じ情報(リピート製品)がDB空間にあったときには、Veが0になり計算できません。その場合、計算できない行以外のηの最大値の数倍を代入するといった近似が必要となります。何倍が良いかという明確な定義はできませんが、事例毎にザックリ決めてみてください。参考までに、私の過去の事例ではη最大値の3倍くらいが「丁度良い具合」でした。
6)閾値よりも大きい値を除外する
Veまたはηについて閾値を決め、
- それを超える値については以降の式に使わない。
- 最も小さいVe(または最も大きいη)が閾値を超える場合には推定値を計算しない。
という処置が必要です。閾値を超えても物理的に計算は可能ですが、閾値外のデータの数が多いほどそれらに引っ張られるため推定精度が落ちます。(平均的な値になってしまいます)
7)推定値を求める
推定値は、各行の真値をηで重み付けして合計します。 閾値から外れた行は無視します。またΣηにおいても同様に閾値以内の行だけの合計です。
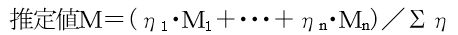
8)項目選択
T法と同じ手順で2水準系直交表を使って項目選択できます。推定精度を上げるためにも項目選択は行っておいたほうが良いでしょう。
項目選択の手順は、ここでは割愛します。MT法の教科書を参照してください。
欠点と改善
計算式を見れば予想できると思いますが、過去データの範囲内でしか推定できません。過去に発生したものより大きく異なるものについては推定できません。
閾値を決めることで、そのデータが推定可能か不可能かの判断もします。精度が悪いと思われる場合(閾値外)には「推定しない」という判断を下したほうが良いでしょう。
この推定には過去の既知情報を使う必要がありますが、その量が多くなると処理速度が遅くなってしまう欠点があります。為替予測のシミュレーションを行ったときは10万行の時間足データから推測しましたが、上記計算式を普通に適用すると計算時間がかなり長くなりました。(都合上5分以上を長いと感じています)そこで、最初に主要と思われる1項目でまずVeを計算して閾値で切り、データ数を減らしてから本計算を行うように改善しました。最初の振り分けだけで10万行が数千行になるので効果は絶大です。これによって15秒程度で計算できるようになりました。ネライは同じことなのでこれくらいの修正は許容範囲と考えます。事例に応じて多少の変更はあっても良いと思います。
適用事例
T法による収縮率の推定とH法
→ 品質工学研究発表大会RQES2013で発表,予稿集内にあり。
品質工学会ホームページからバックナンバーを購入できます。