ＭＴ法

特徴

ＭＴ法はパターン認識の手段として提案されました。正常と異常を区分けするための手段です。よって、定量的な値を求めるのではなく、正常なものにどれだけ近いかといった距離（マハラノビスの距離）を計算します。この距離はインドの数学者マハラノビス氏によって考案されたもので（ＭＴ＝マハラノビス・タグチの頭文字）そこにシュミットによる項目選択の考え方を融合させたのがＭＴ法です。

計算式の考え方

ＭＴ法を紹介するための有名な例は、
トルストイの有名な小説「アンナ・カレーニナ」の冒頭の一行
「幸福な家庭は皆同じようだが、 不幸な家庭はそれぞれの事情が様々である」
いろいろなケースの不具合を予測することは困難だということです。

そこで、多種多様な異常を予測するのではなく、
正常な状態を確立しておき（基準空間を作り）、それからの差で評価することでどんな種類の異常であろうが、正常との違いの度合いで評価する、というものです。

わかりやすいように、例えば２項目だけで表現してみます。
Ａ.身長とＢ.体重を例にして説明すると、

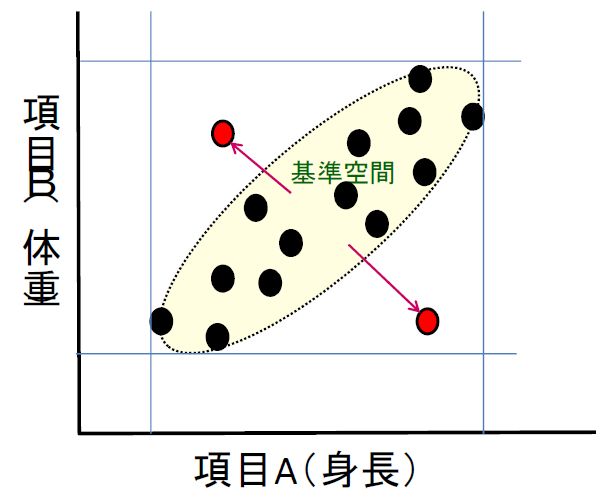
標準的な体型は、図の黄色○で囲われた人です。
右下の赤丸は、身長が大きいが体重が軽い　＝　ヤセ形の人
左上の赤丸は、身長が低いのに体重が重い　＝　太りすぎの人
身長と体重の絶対値で区切ろうとすると、赤丸は規格内に入ってしまいます。
黄色○からの距離で評価してやろうという考え方になります。
例は二次元なのでわかりやすいですが、多次元空間でこれを計算するわけです。

具体的な計算手順

・評価したいデータを準備する（項目を決める）
・基準となるデータと比較したいデータを分ける
　※何を基準と考えるかが重要！基準となるデータを基準空間データと呼ぶ
・項目毎に平均値と標準偏差を求める

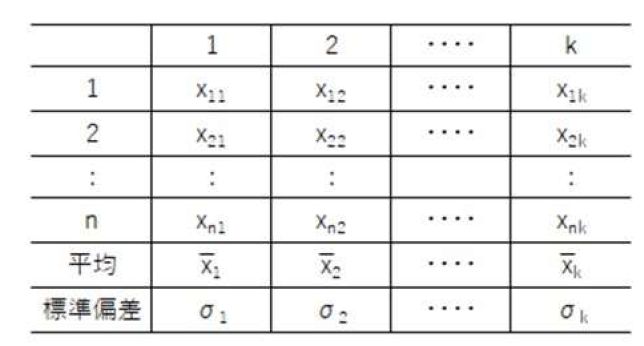
・規準化する

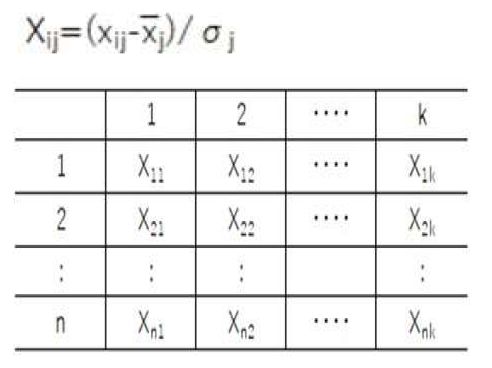
・相関行列を計算する
・逆行列を計算する

・各データのマハラノビスの距離（Ｄ2）を計算する
（基準空間データ，比較データ）
・計算したマハラノビスの距離でヒストグラムを作成
・閾値を決める

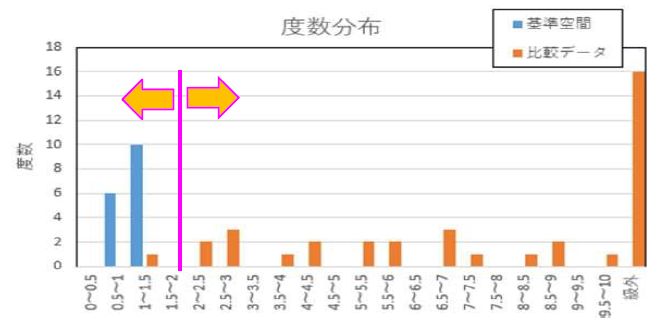
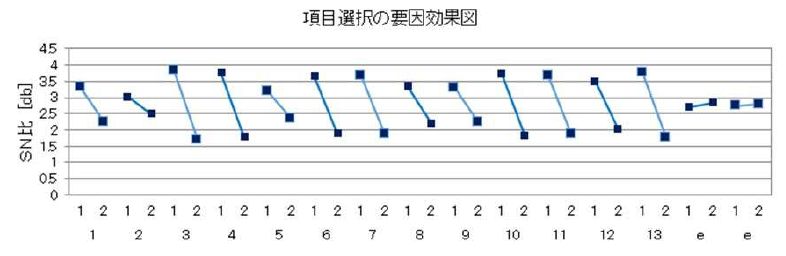
・項目の効果を確認するときは
1）項目数に対応した大きさの直交表を選択する
2）直交表に従って使用する項目で計算する
3）各行のＳＮ比を計算して要因効果図を作成する
4）不要な項目は削除するとよい
注意:比較データに対する傾向であり、 全ての誤差を推定するものではない