特徴
T法(1)は定量的な値を推定したいときに使います。過去データや製造履歴から、未来の値,製造後の特性や歩留まりなどを予測します。T法には(1)から(3)までありますが、T法(3)は計算式が全くことなるので別で解説します。T法(1)と(2)の計算手順は同じで、(1)は単位空間を中央にとる場合,(2)は単位空間を端にとる場合です。
計算式の考え方
T法は、項目と結果との比例関係(y=βM)について、ばらつきで重み付けしながら足し合わせる計算方法です。イメージを下図に示します。
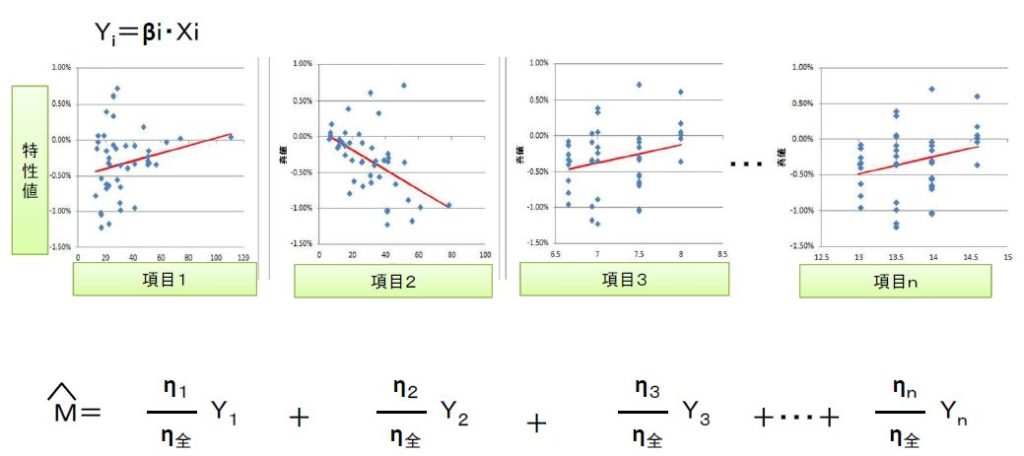
各項目毎に、結果との比例式を作ります。y=βMの関係式を計算します。データを規準化(平均値を引くだけ)しているので、基準点比例式となります。特性値,項目の中心(平均値)を座標(0,0)とした基準点比例式です。
この計算をすると、傾きβとばらつきη(σ/β)が計算できます。ばらつきが小さい(ηが大きい)項目の意見を多く取り入れるよう、重み付けをします。それが、上の式のηi/η全です。
当然ながら、全く比例関係が無い項目は削除すべきです。それは後から直交表を使ったシュミットで判定することができます。弱くともなんとなく比例関係があれば、それを推定計算に取り入れます。
計算はy=βMがベースになっているので、項目と特性値との関係に直線関係が無いと正しく推定できません。よって、項目を考えるときに、直線関係が得られるように変換するなどの工夫が求められます。
具体的な計算手順
・基本となるデータを準備する(項目を決める)
・単位空間データと信号データに分ける
未知データも準備しておくと良い
単位空間は、ばらつきの中心などにすることが多い
・単位空間で項目毎の平均値を求める
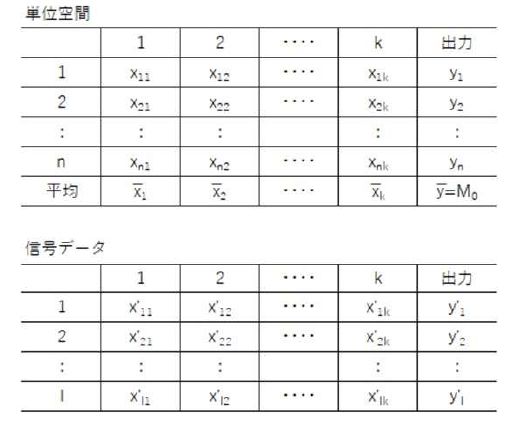
・データを規準化する(平均値を引くのみ)
・項目ごとにSN比ηとβを求める

・総合推定値を計算する(未知データも含めると良い)
・真値と推定値との差は散布図などで視覚化すると良い
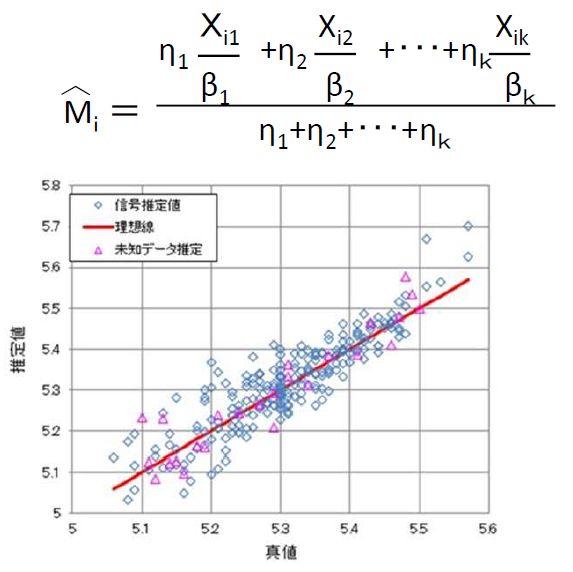
推定誤差をSN比で計算する

直交表を使って項目の重要度を評価する
1)項目数に対応した大きさの直交表を選択する
2)直交表に従って使用する項目で計算する
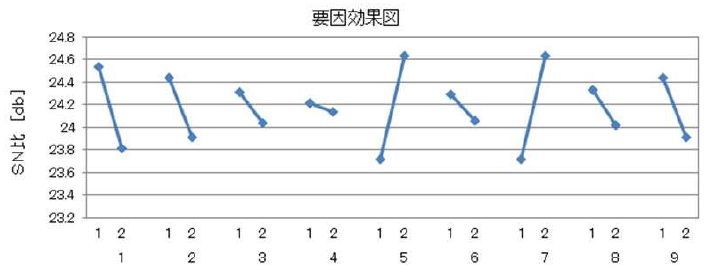
3)各行のSN比を計算して要因効果図を作成する
4)SN比を悪くする項目は削除するとよい