思考大会・小学生の問題を解いてみた・令和2年度の超難問

思考大会独特のパターン化の問題です。
まずは1→4，2→12，3→20･･･5→48という
数字の並びについて、
どんな法則が成り立っているか考えるのですが、
簡単ではありません。
問１くらいなら問題図に●を書き込んでいって
数えることができるでしょう。
（力ずくの解答）
問1の解答＝84個
問２を解くにはもう一歩、
補助的な「何か」が必要です。
あれこれ悩んだ末、
下図のような式の羅列で考えるのが良いのでは？
と思い書いてみました。

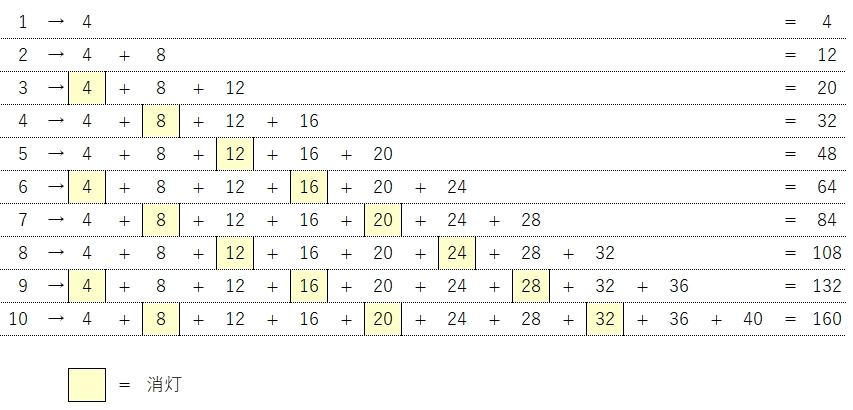
手書きでもこれくらいは書けます。
これでようやく問２を解くことができました。
問２の解答：１６０個
しかし、この方法で問３は厳しい。
もっと法則性を、わかりやすい式か図に
現したいところですが、
なかなか難問です。
・・・手書きが大変なので
EXCELでやってみました。m(_ _)m

まずは消灯を無視して、
増える点灯数をまとめます。
4,12,24･･･と増えていきます。
４の倍数になっていそうなので
４で割ってみます。
すると、1,3,6･･･と意味深な並びに。
10で55になることに着目すると、
n分後までの数値の合計だと気付きます
（数式を使えばnの階乗＝ｎ！）。
例えば５分後なら
1+2+3+4+5=15で15×4=60
が点灯する数の合計。

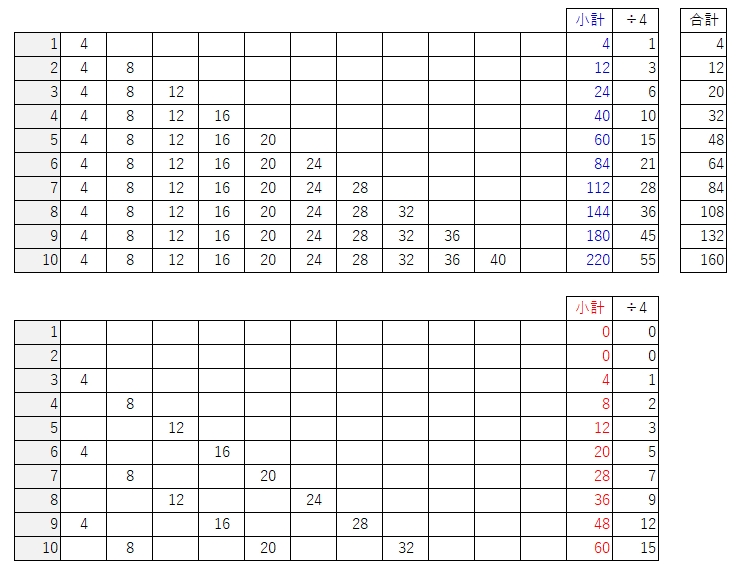
消灯する分は法則がすぐ浮かびません。
そこで、単純に表にして計算してみることに。
消灯する部分は下図ⅠⅡⅢ･･･として増やしていきます。

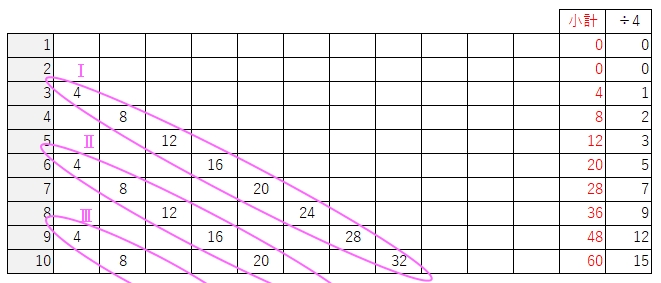
下の表の青字部が点灯の増える分，
赤字部が消灯する分，
その全ての合計が答えとなります。
よって、問3の解答：1114個を超えるのは28分後
なお、下表右端の合計は
全て計算する必要は無く、
きりのいいところだけ計算すれば
効率的に答えにたどり着けます。

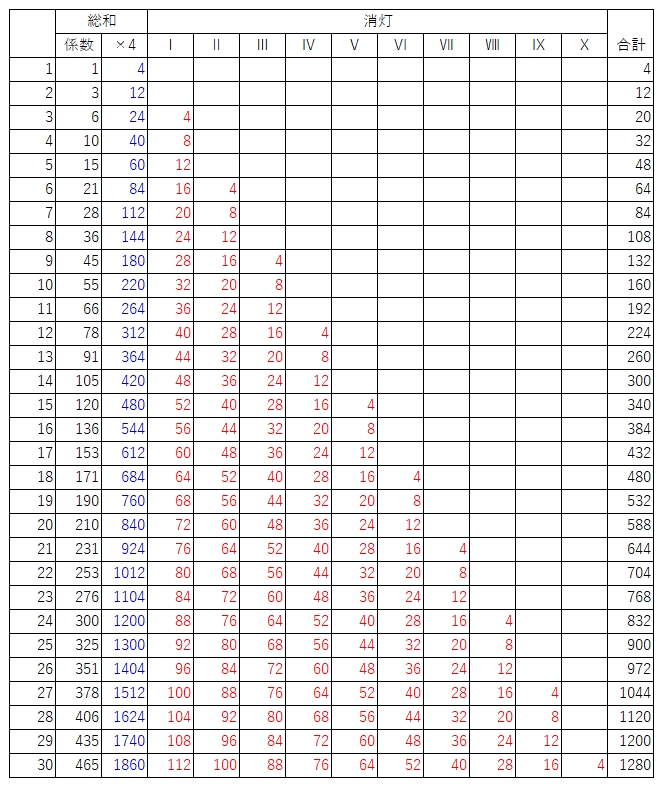
このデータをグラフ化して
図示のイメージを示します。
小学生なので図形思考で解答を導く，
というふうにイメージしたいのですが、
ちょっとスッキリしませんね。

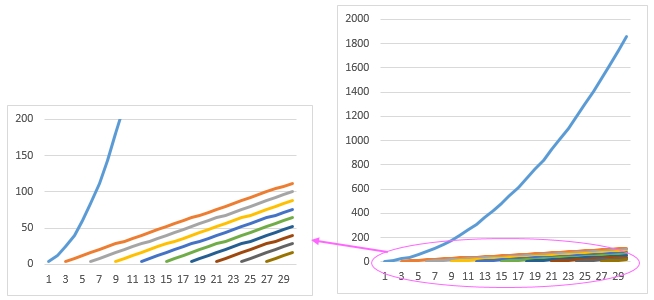
消灯するほうを、もう少し
公式化してみたいところです。
表の右側に補助表を作ってみました。
消灯の合計を４で割った数字は、
少しずつ増えていきますが
単調増加ではなく指数的に増えています。
そこで、
増えた量をその右側に計算すると、
0,0,1,1,1,2,2,2,3,3･･･と3個毎に1
増えるようになっています。
これを利用すればｎ分後をもう少し
早く計算できるかもしれません。
参考まで。

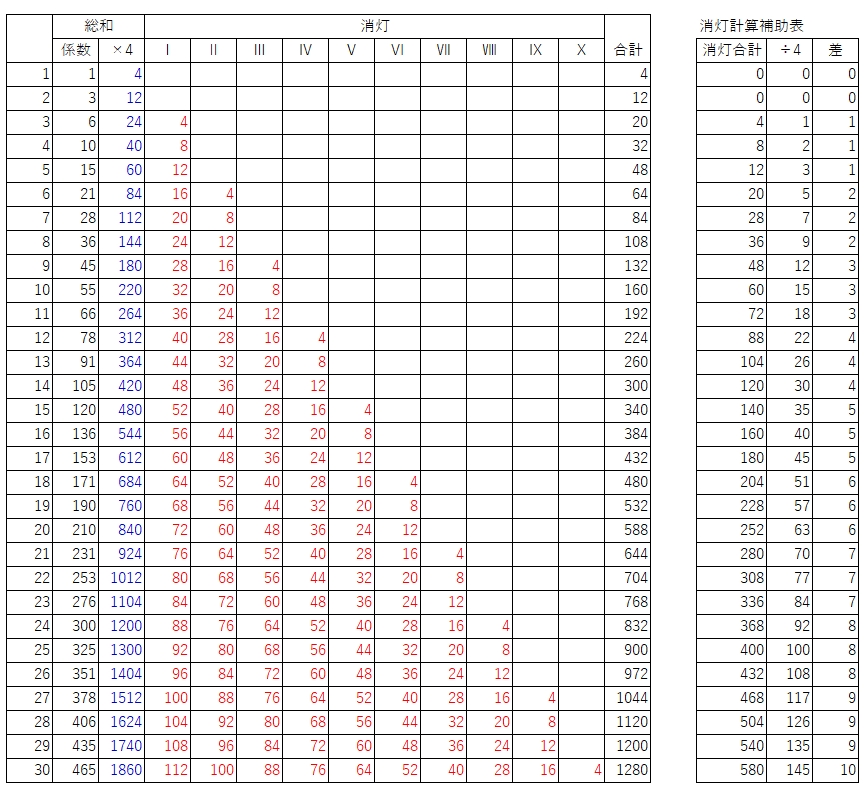
EXCELを使って計算してみましたが、
これをパソコンなしで、
電卓なしで（限られた時間内に）
解答するのは、
私には難しいですね。
しかし、
この問題の正答率は4.5%だったので、
解答できた小学生が
何人かいたということです。
すごい！
と思うしかありません。。

美人女子大生Yunさんの回答

この問題を、
美人女子大生のYunさんに
解いてもらいましたら、
なんと、
10分くらいで解いてしまいました。
私の身の回りの何人かに問題を出してみたのですが、
ほとんどの人がお手上げ状態だったので、
その優秀さにとても驚き、
同時にとても感心しました。
しかし、
解答はあくまで地道な加算を繰り返した
とのこと。
そこで、公式化できるものか
やってみてもらいました。
少し時間がかかりましたが、
見事に数式化できましたので
（EXCELでも検証済み）、
以下に紹介します。

まずは点灯する全てのランプの
個数を求める。（消える分を除く）

ｎを使った数式にしたい。
1分→4個，2分→2×6個，3分→3×8個，4分→4×10個，5分→5×12個
2ずつ増えている＆2の倍数（偶数）
式にすると　2n＋2
つまり、
点灯する全てのランプの個数を
nを使って表すと n(2n+2) = 2n(n+1)

次に消えたランプの個数を求める。

n が 2 より小さい時は消えたランプが 0 なので、
n が 3 以上の時を考える。
3回ごとに数字の増え方が変わっている。
→数字の変わるタイミングは
3 の倍数になった時！
3の倍数，3で割ったとき余り1，
3で割ったとき余り 2
で場合分けして考える。

① 3の倍数のとき

nが3の倍数の時なので整数ｍを用いて表すと
n = 3m となり m = n/3 となる。
つまり、
mはnを3で割った時の答えと表すことができる。
mが1のとき4，mが2のとき20，mが3のとき48･･･　
これを数式で表すと
am = 4, 20, 48 ･･･ となる。
この数列の一般項を求める。
このままでは求められないので
数列の各項の差である階差数列を使う。
階差数列を｛bm｝とすると、

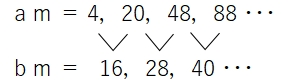
まずbmの一般項を求めると
bm = 16 + ( n – 1 ) ×12　= 12n + 4
求めたbmを使ってamの一般項を求める。

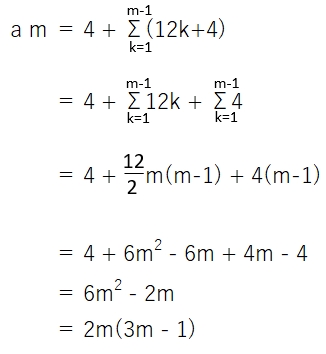
② 3で割ったとき余り1 のとき

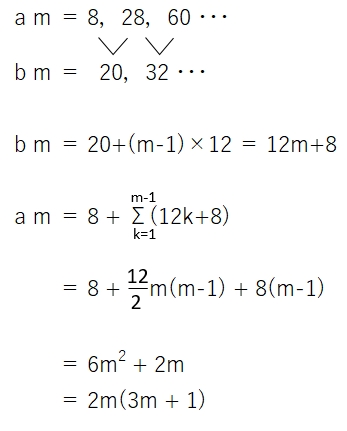
③ 3で割ったとき余り2のとき

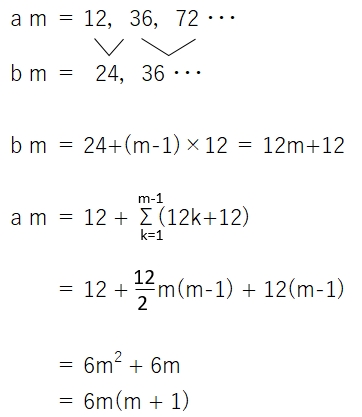
よって、数式を以下にまとめると、

[1] n < 3 のとき
　2n(n+1)

[2] n >= 3 のとき
　ｎを3で割った時の答えをｍとすると、
　① ｎが3でわりきれるとき
　　　2n(n+1) – 2m(3m-1)
　② ｎを3で割った時の余りが 1 のとき
　　　2n(n+1) – 2m(3m+1)
　③ ｎを3で割った時の余りが 2 のとき
　　　2n(n+1) – 6m(m+1)