富山県に「富山県児童生徒思考大会」という事業があるようです。さすが、教育に力を入れている県ですね。1957年に「人間に与えられた特権ともいえる『考える』ということの大切さを強く意識し、じっくり考える機会を子どもたちに与えよう」と始まったとのこと。小学生(5~6年)の部門と中学生の部門があります。6問程度を2時間で解いて正解率を競います。情報分析力やひらめきが求められる問題です。
こういう問題があると聞くと思わず「解いてみたい」と思うのは私だけでしょうか?算数好きの人であればきっと楽しめること請け合いです。先日HPからダウンロードした令和元年度の問題を解いてみたのですが、その中からひとつだけ面白そうなものをここに掲載します。私の回答を下に示していますが、それが正解かどうかはわかりません,参考です。
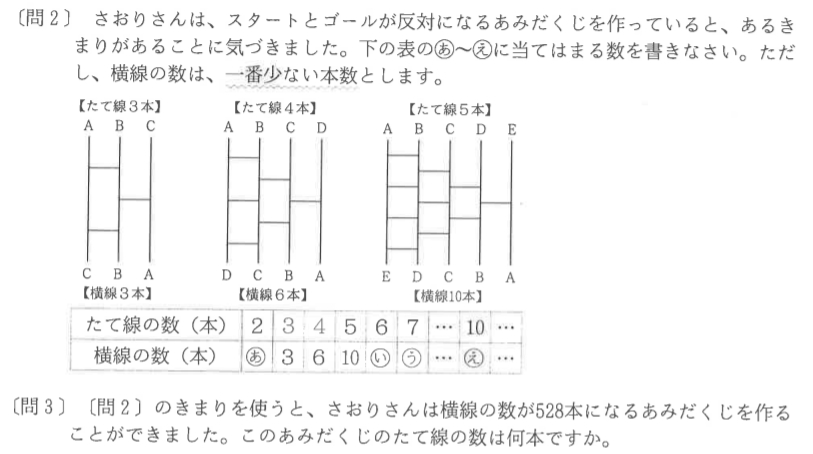
[問2]は簡単ですぐにわかると思います。
縦2→横1,縦6→横15,縦7→横21,縦10→横45
そして、これに法則を定義するのが[問3]ですね。
私が考えたイメージは三角形の面積です。
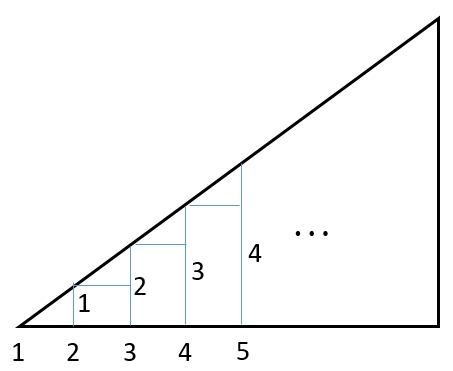
図のように、縦の値を1辺として、直交するもう1辺の値を「縦の値-1」とする三角形の面積になるのではないかとイメージしました。
三角形の面積は「底辺×高さ÷2」ですから、
縦7のときなら、7×(7-1)÷2=21
縦10のときなら、10×(10-1)÷2=45
この考え方で、答えが528になるものを考える。
528=縦の値×(縦の値-1)÷2 → 1056=縦の値×(縦の値-1)
この式で、それに当てはまる縦の値を、あとは試行錯誤でやってみれば良い。
中学生になれば、イメージを方程式で定義できるでしょう。
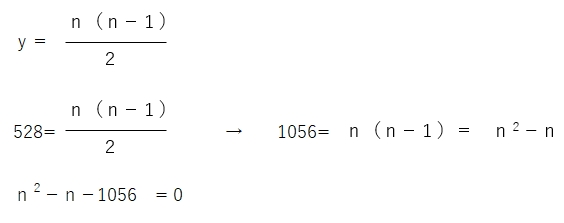
2次方程式を解けば、n=(1±65)/2となり、解は 33 と -32 と導け、
マイナスは無いので答えの33を算出できます。
しかし、小学生では(当然ながら)2次方程式の公式は知りませんし、
記号を使った表現も不可,平方根の計算(ルート4225)もできません。
私も大きい数値の平方根が計算できず(長らくやっていなくて忘れてしまいました・・・普段はEXCELでSQRT関数で処理しますから・・・)
検証に思わずパソコンを使ってしまいました。
さて、小学生の場合の解き方,中学生だったら、と2種類の解法を挙げてみましたが、地道に足していってもいちおう解けます。問題図では縦線の数10まであるので、33まで道のりは長いですが(だから上述のような苦労をしているわけですが)そろばんをやっていた子とか暗算が得意な子なら、それ(地道に528になるまで足していく)もアリでしょう。
学者のように数式にすることが美学というわけではなく、大会の問題なので、早く回答できることが重要,とすれば地道に足し算していっても、そのほうが早ければ、それが最善手です。
個人的には、論理的に説明できる式を導くことに楽しさを感じますが。。。