ボリンジャーバンドの計算に使われる標準偏差、どんな計算をしているのか詳細に解説します。
説明しやすいようにデータ数を少なめにした 5 pointでの計算で例を示します。
期間数を5にしたローソク足のデータが図のように微増傾向で、値が、
13 , 11 , 14 , 12 , 15
のように変動したとします。
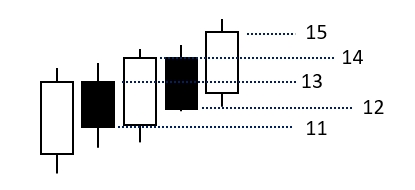
この期間の平均値は、(15+14+13+12+11)/5=13 です。
この5個のデータは、平均的な値と、平均からの差に分解できます。

ここから、少し難しいですが、2乗和の分解についての説明です。
ばらつきの総量を全変動といい、記号STであらわします。
平均(偏りの大きさ)総量は一般平均といい、記号はSmです。
個々の値と平均との差は、誤差変動または個体差変動といい、記号はSeです。
それぞれの計算式は以下の通りです。
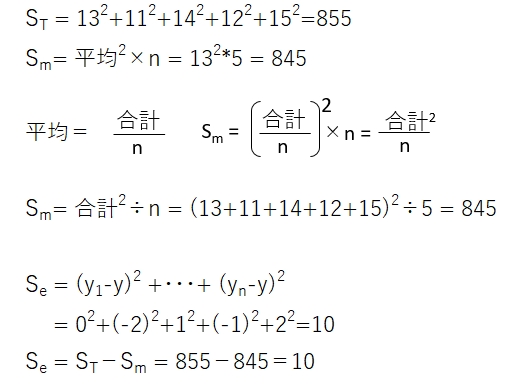
SmとSeは2通りの式を記載していますが、よく使用されるのは2回目に記載したほうです。全変動=平均変動+誤差変動になる、というのが2乗和の分解で、詳しい検証展開は記述しませんが、容易にできると思います。
Seが誤差(ばらつき)の変動合計なので、平均的なばらつきを求めたいと思います。何に対する平均を求めるかといえば、自由度です。自由度とは、変動の計算における未知数の数で、実質的な2乗の個数として求めることができます。
各自由度は以下の通りで、ここでも自由度の足し算が成立します。
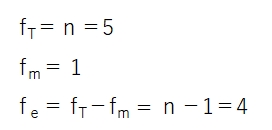
自由度1あたりの変動を分散といいます。記号はVを使います。
分散の平方根はデータの広がり方をデータの次元で示すもので標準偏差といわれています。記号はσやsが使われます。
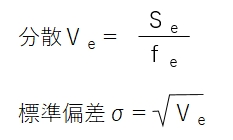
品質工学ではエネルギー分解を評価するので、2乗和の分解とVまで使います。
一般的な品質管理では標準偏差σを使うことが多いですね。ばらつきが正規分布に近似していれば、確率計算できます。
ボリンジャーバンドの計算は、この標準偏差σを使っています。
まじめに計算するなら、傾きを求めて信号に対する誤差を計算すべきでしょうが、どこから傾きが始まったのか?そのタイミングは上昇に向かったのかばらつきなのか?といったことが不明なので、とにかくザックリ全てのデータを標準偏差で計算して、値(σ)の変動を視覚的に観察する、という発想は面白いと思います。